By: Dan Falk
8 Jun, 2017
Quantum Insecurity
June 8, 2017
The ability to send gigabytes of data around the planet in the blink of an eye has transformed our world. But it comes with great risk.
How do we keep files safe and secure as they zip from computer to computer and country to country? For years, we have relied on encryption systems using math problems so difficult that even a supercomputer can’t solve them without the key. But this tried-and-true method may soon be obsolete, thanks to quantum computers.
“We need a stronger cyber immune system,” says Michele Mosca, because our current systems have reached “an unprecedented level of vulnerability.” Mosca, a senior fellow in CIFAR’s Quantum Information Science program and co-founder of the Institute for Quantum Computing (IQC) at the University of Waterloo, is on a mission – to raise awareness of this cyber vulnerability before it’s too late.
Attack at Dawn
Cryptography – the coding and decoding of secret information – certainly predates computers. Substitution ciphers, where one letter is replaced by another according to a fixed rule, have been used since ancient times.
An example: ATTACK AT DAWN becomes CVVCEM CV FCYP if each letter moves two places to the right in the alphabet. (It is said that Julius Caesar used such a code in his personal correspondence.) In the example above, it only takes a minute or two to encode a short message by hand; but decoding it requires a good deal of patience, as one tries various possible substitutions. Decoding, by its very nature, is the hard part. That’s the whole idea.
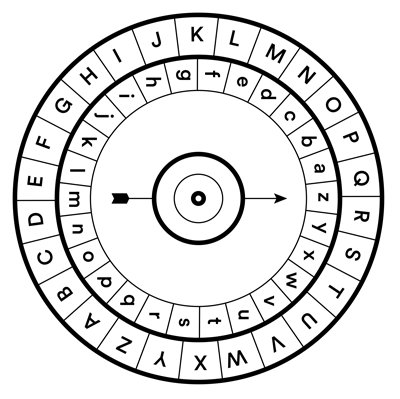
Early cryptologists used “cipher disks” for simple substitution codes. Quantum computers could make modern encryption just as insecure.
Today’s most widely used encryption techniques are mathematical at heart. One common technique exploits the basic fact that it’s much easier to multiply two large numbers than to take the result and work backwards. You can use a pocket calculator – or pencil – to find out that 1,307 x 2,153 = 2,813,971. But, given the number 2,813,971, you’d be hard-pressed to work out its divisors (which, in this case, are both prime, so they’re the only ones possible). You can program a computer to figure it out, of course. But if the number you want to factor is large enough, even this becomes nearly impossible.
“It takes, effectively, forever to take a 1,000-digit number and find its prime components,” Mosca says.
For decades now, we’ve been trusting all manner of sensitive information to this sort of coding, even when we’re not aware of it. Your web browser does it for you whenever you make a secure connection with your bank, buy something on Amazon, or even do a Google search. We trust everything to it – from credit card transactions to intellectual property to government secrets. And it all has the potential to fall into the wrong hands if the codes are hacked.
Enter the quantum computer. Researchers worldwide are trying to apply the principles of quantum mechanics to build computers that will do things existing computers simply can’t. Unfortunately for electronic security, one of the things quantum computers may be able to do is factor large numbers almost instantly.
Bits and Qubits
In a conventional computer, the basic unit of information (the bit) can be either on or off, zero or one. But a quantum bit, known as a qubit, can be in a “superposition” of two states at once – a zero and a one at the same time. (See Figure next page). As a result, the power of a quantum computer could expand exponentially in proportion to the number of qubits: two qubits performing four calculations at once; three performing eight; four performing 16 – and so on. This gives quantum computers the potential to vastly outperform classical computers on certain kinds of tasks.
“There are certain problems they could solve very quickly that a classical computer would have to do a lot of work, using the best-known algorithms, to solve,” Mosca says. But he adds that a working quantum computer would not be a magic bullet, able to solve any mathematical problem ever devised. “For most tasks, there’s really no speed-up. But for some very important tasks” – such as factoring large numbers – “there’s an astronomical speed-up.”
Algorithms already exist for tackling such problems with a quantum computer. “Shor’s algorithm,” one of the first, was developed in 1994 by American mathematician Peter Shor. A number that might take a billion years for a classical computer to factor could be factored by a quantum computer in about one second, using Shor’s algorithm. (The time required would be roughly proportional to N3 , where N is the number of bits in the number being factored; while a classical computer would require a time proportional to 2N . As N increases, 2N becomes astronomically larger than N3 , and the “quantum advantage” becomes enormous.)
How far are we from a fully functional quantum computer? Major challenges are still being faced. First, qubits need to be “stable” – that is, they need to be isolated from their immediate environment so they can maintain their superpositions for longer than a fraction of a second. Also, they need to interact with other qubits in a controlled way. And then there’s error correction. Every time a bit is processed, there’s a chance of making a mistake.
In classical computing, error correction can be dealt with through redundancy – encoding a 0 as 000, for instance, so that if one bit accidentally flips to a 1, the other two bits still show the correct value. Error correction isn’t as easy with quantum computers. To duplicate a qubit you would have to measure it first, but that would collapse it to a single value and you would lose the advantage that qubits give you in the first place. So scientists have had to figure out other ways. For instance, one method “spreads out” the information for one logical qubit over nine physical qubits, allowing subtle measurements that can detect an error without actually disrupting the value being stored. Using these techniques and others, engineers and computer scientists at the IQC and other labs are making progress, gradually taming the problem of qubit errors.
Mosca believes we’re getting close to a working quantum computer. As we spoke in his office at the IQC this winter, he outlined the seven stages on the path. The first stage is simply the encoding of qubits; the second stage is getting multiple qubits to interact; the third stage is successfully managing error correction. Fourth: getting that error rate down to the point where your system can function as a “logical bit,” the equivalent of a vacuum tube in our first computers. Next: having two of these bits. Next: having many. Finally, at stage seven, you have a full-fledged, fault-tolerant quantum computer.
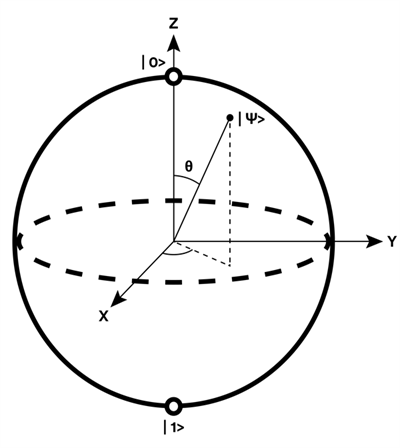
The Bloch sphere represents how a qubit can be in a superposition of both 0 and 1.
“I think we’re really close to stage four,” Mosca says. “But people are already starting to anticipate stages five, six and seven – which will have a lot of engineering challenges.”
There are many reasons to be excited about the arrival of quantum computers. The problems they’re best suited to – juggling huge numbers of combinations, in search of certain patterns – will make them ideal for designing materials, buildings and even the molecular structure of drugs. But, as noted earlier, this also means the power to break codes – including the publickey encryption that we currently use to protect everything from credit card transactions to government secrets.
Mosca estimates a one-in-seven chance that some of the fundamental public-key cryptography tools we rely on today will be broken by 2026. And he sees it as a 50 per cent chance by 2031. He says the solution is to move beyond the techniques that underlie today’s encryption tools, such as the factoring of large numbers. He doesn’t believe quantum computation will actually kill off public-key cryptography, but he says it will force us to find more sophisticated encoding techniques. “We think it’s possible. We just need to find the right kind of mathematical problems.
“There’s a small group of mathematical problems that seem to have the necessary properties where they resist quantum attack. They’re hard one way, easy the other way, if you have the private key.”
Lattice problems, for example, are a class of optimization problem that involve paths between points on a regular array. Like factoring, these kinds of problems can be easy to do one way, and very hard to do the other. (See illustration next page.) These investigations are just beginning. Very little study has been aimed at determining which techniques are the most resistant to quantum cracking. Whatever system is developed will need to be “battle tested,” Mosca says. To that end, he and Douglas Stebila, an assistant professor of cryptography at McMaster University, have launched an open-source software project. Called Open Quantum Safe, its focus is on the development of prototypes of quantum-resistant cryptography.
Fighting Quantum with Quantum
Quantum mechanics led to the problem in the first place – and may also point the way to a solution. A method called quantum key distribution, for example, would use quantum mechanics to let two people generate a secret key, but over public networks. This would rely on a quantum property called entanglement, in which two particles are entangled so that if you measure one of them, you also learn the measurement of the other.
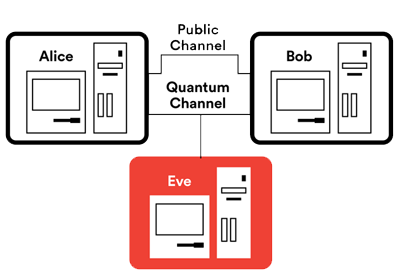
Using quantum key distribution, Alice and Bob first establish a private key using a secure quantum channel, and then use the key to encrypt their communication over a public channel. If Eve tries to eavesdrop onthe quantum channel, the laws of quantum physics guarantee that Bob and Alice will be able to tell.
In simplified terms, it would work like this: You exchange entangled particles with the person you want to communicate with, and measure the particles you receive until you’ve both taken enough measurements to create a strong key. If a third party tries to eavesdrop during this process, you’ll detect a disturbance in your measurements. You’ll keep trying until you have generated a key that you know is safe, i.e., until you’re sure no one else has a copy.
CIFAR fellows have made important contributions in this area. Senior Fellow Gilles Brassard and Advisor Charles Bennett developed the very first quantum key distribution protocol in 1984. More recently, CIFAR Fellow Thomas Jennewein has experimented with sending entangled pairs long distances through the air and over fibre optic cables. He hopes to soon generate them from a satellite in Earth’s orbit. And a team led by Senior Fellow Wolfgang Tittel of the University of Calgary succeeded in “teleporting” the quantum state of a photon six kilometers over Calgary’s municipal fibre optic network, an accomplishment that could lead to eavesdropproof communications networks.
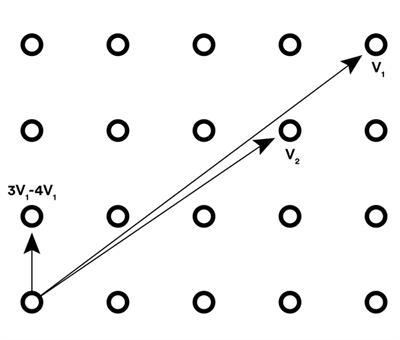
The shortest vector problem is an example of a problem that is easy to do one way, but not the other. In the problem you’re given lines, or vectors (v1 and v2), from one point to two other points in a lattice. The problem is to figure out the shortest non-zero vector in the lattice – that is, the line that connects the starting point to its nearest neighbour – expressed in terms of the two vectors you’ve been given. Although it looks simple in the illustration, like factoring large numbers, it quickly becomes computationally difficult.
Although our encryption systems are quickly becoming vulnerable, Mosca says we are being presented with an opportunity – as long as we understand the danger. For years he has been speaking to business and government leaders, alerting them to the threat. One sign that the message might be getting through: Last year in the U.S., the National Security Agency (NSA) announced a plan to overhaul its encryption systems to defend against high-level cyber attack. This public announcement by the usually secretive NSA shows that they’ve recognized a serious threat, says Mosca. “They made it clear they’re going to require quantum-resistant algorithms in the near future. That was a huge wake-up call for many people.
Of course, we’ve been saying this for years. And I think it has stimulated organizations, particularly within the U.S., to come up with a plan.” Cyber security isn’t cheap, of course. Defending against the attacks that a quantum computer could enable will require significant investment. But as Mosca points out, not acting can have its own costs, and they can be enormous. A cyber attack could be truly devastating, he says. “It has the potential to undermine everything, from your democratic institutions to bleeding billions of dollars out of your country’s economy.”
When Mosca meets with government and business leaders, he explains that spending money now to prevent attacks in the future is a large but necessary investment. He just hopes that the message gets through soon.
Photo: Markian Lozowchuk
Related Articles
-
Bugs, Babies & Brains
June 13, 2024
-
How do we create a google map of the human body?
June 13, 2024
-
How does the brain give rise to the mind?
June 13, 2024
-
A day with Kristin Andrews
June 13, 2024